O trapézio é um polígono de quatro lados com dois lados paralelos. Para calcular a área de um
trapézio, precisamos conhecer a medida de sua base média. A base média de um trapézio é a medida da linha reta que une os pontos médios dos lados não paralelos. Neste artigo, vamos explicar como calcular a medida da base média de um trapézio.

Considere um trapézio com lados paralelos medindo b₁ e b₂ e altura h, como mostrado na figura abaixo:

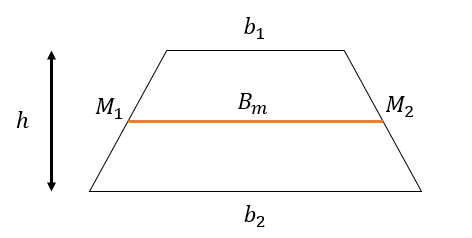
Os pontos médios dos lados não paralelos são denotados por M₁ e M₂, como mostrado na figura acima. A base média do trapézio é a medida do segmento de reta que une M₁ e M₂.

Para calcular a medida da base média, usamos a seguinte fórmula:

\begin{equation*}
B_m = \frac{b_1 + b_2}{2}
\end{equation*}

Ou seja, a base média é igual à média aritmética das medidas dos lados paralelos.

Vamos aplicar essa fórmula em um exemplo. Considere um trapézio com lados paralelos medindo 8 cm e 12 cm e altura 6 cm como na figura abaixo:

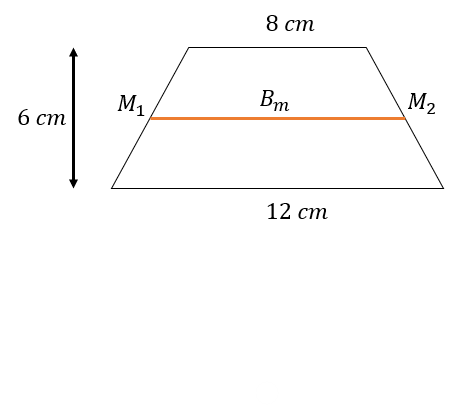
Para calcular a medida da base média, usamos a fórmula:

\begin{equation*}
B_m = \frac{8 + 12}{2} = 10
\end{equation*}

Portanto, a medida da base média do trapézio é 10 cm.

É importante ressaltar que a base média de um trapézio é uma medida importante para calcular a área do polígono. A área de um trapézio pode ser obtida através da fórmula:

\begin{equation*}
A = \frac{(b_1 + b_2)\cdot h}{2}
\end{equation*}

Onde b₁ e b₂ são as medidas dos lados paralelos e h é a altura do trapézio. No caso do exemplo acima temos

\begin{equation*}
	B_m = \frac{(8 + 12)\cdot 6}{2} = 60,
\end{equation*}

ou seja, a área do trapézio é 10 cm²

Concluindo, a medida da base média de um trapézio é a média aritmética das medidas dos lados paralelos e é uma medida importante para calcular a área do polígono.